Union Find
Remarks
- Union Find is a data structure keeps track of a set of elements that are partitioned into a number of disjoint subsets.
- It has two operations
union(p, q)andfind(p).- the find/search finds the subset element
pbelongs to. - and union/merge merges the subsets containing
pandq.
- the find/search finds the subset element
- It memory usage is O(N), and each find and union operations are near O(1) in time.
- The algorithm can be used to find all connected components in a network. Compare to DFS/BFS for finding connected components, UF is better suited for dynamic connectivity where edges can be added overtime and the components info can be queried at any given time.
- It is also used in kruskal’s algorithm to find the minimal spanning tree for a graph.
Implementation
Simplest implementation to use the core of union find.
parents = list(range(n))
def find(i):
if i != parents[i]:
parents[i] = find(parents[i])
i = parents[i]
return parents[i]
def union(x, y):
x, y = find(x), find(y)
if x == y: return
parents[x] = y
return y
Define a class for UF
class UnionFind:
def __init__(self, n):
self.parents = list(range(n))
self.sizes = [1] * n
def _find_recursive(self, i):
while i != self.parents[i]:
# path compression, have i points to the cluster centroid
self.parents[i] = self._find_recursive(self.parents[i])
i = self.parents[i]
return i
def _find_iterative(self, i):
# 1 path to find the root
root = i
while self.parents[root] != root:
root = self.parents[root]
# 2 path to assign every node in the path to points at root
while self.parents[i] != root:
parent = self.parents[i]
self.parents[i] = root
i = parent
return root
find = _find_recursive
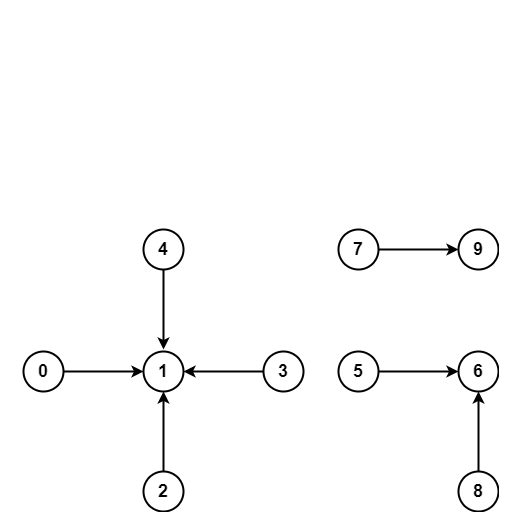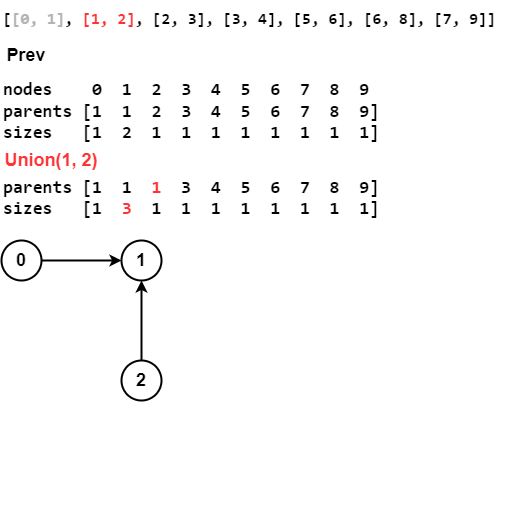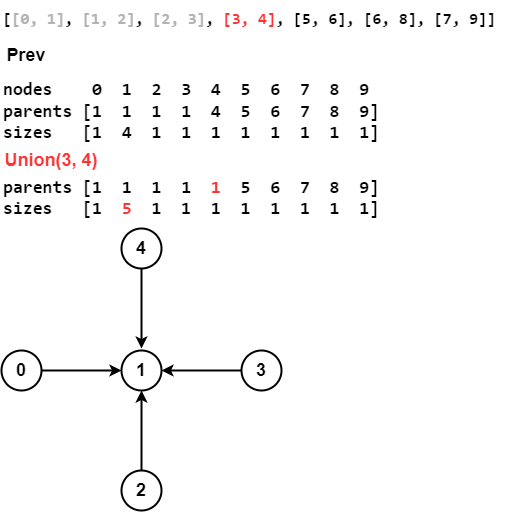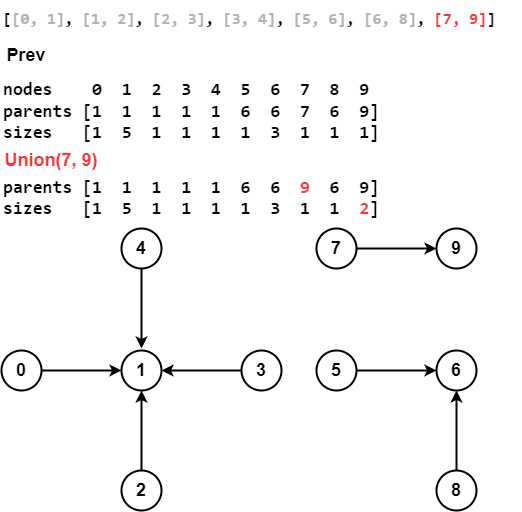
def union(self, p, q):
"""Attempt to union two elements
Args:
p, q: two elements to be attempted for union
Returns:
Boolean indicates whether a union operation is performed.
"""
root_p, root_q = map(self.find, (p, q))
if root_p == root_q: return False
small, big = sorted([root_p, root_q], key=lambda x: self.sizes[x])
self.parents[small] = big
self.sizes[big] += self.sizes[small]
return True
Use Union Find to find connected components in undirected graph.
connections = [[0, 1], [1, 2], [2, 3], [3, 4], [5, 6], [6, 8], [7, 9]]
uf = UnionFind(10)
for p, q in connections: uf.union(p, q)
num_components = len(set(uf.find(i) for i in range(10)))
print(num_components)
- To find minimum spanning tree in the graph where there are weights on the edges.
- Sort edges by edge weights ascendingly.
- Iteratve over the edges unify nodes when two nodes don’t belong to same cluster.
- Repeat 2 until no nodes or no edges.
An Implementation without pre-allocation
class UnionFind:
def __init__(self):
self.parents = dict()
self.sizes = dict()
self.n_sets = 0
def __contains__(self, i):
return i in self.parents
def insert(self, i):
if self.__contains__(i): return
self.parents[i] = i
self.sizes[i] = 1
self.n_sets += 1
def find(self, i):
while i != self.parents[i]:
self.parents[i] = self.find(self.parents[i])
i = self.parents[i]
return i
def union(self, p, q):
"""Attempt to union two elements
Returns:
Boolean indicates whether a union operation is performed.
"""
root_p, root_q = map(self.find, (p, q))
if root_p == root_q: return False
small, big = sorted([root_p, root_q], key=lambda x: self.sizes[x])
self.parents[small] = big
self.sizes[big] += self.sizes[small]
self.n_sets -= 1
return True