Binary Tree Traversals
Remarks
class Node:
def __init__(self, val=None, left=None, right=None):
self.val = val
self.left = left
self.right = right
root = Node(1)
root.left = Node(2, left=Node(3), right=Node(4))
root.right = Node(5)
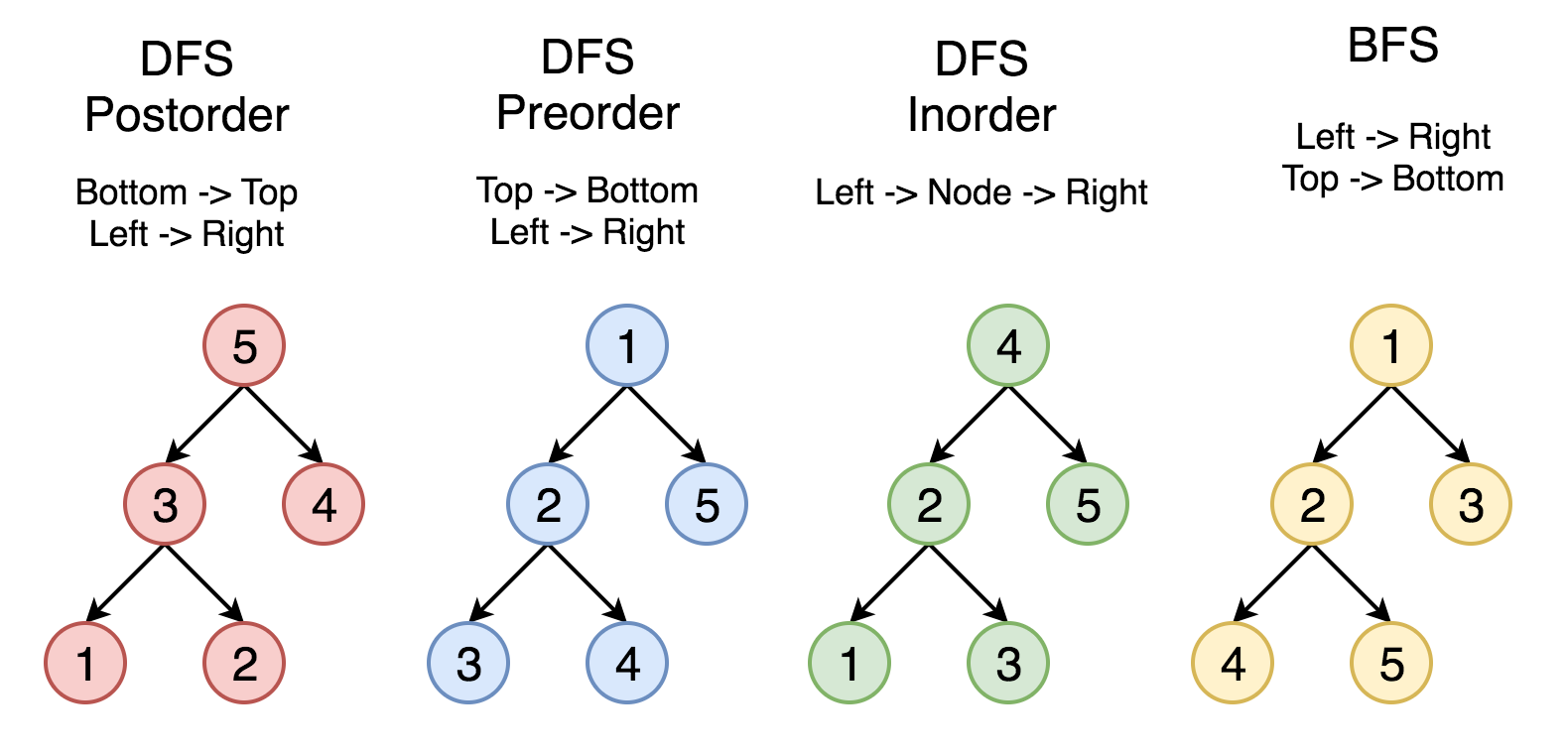
DFS traversals
- Recurrsive implementation of the tree dfs traversals are pretty easy.
- Iterative implementation:
- Inorder and preorder relatively straightforward implementation with stack of node pointer alone.
- Postorder would need some additional help.
- With an boolean backtrack indicator, or with a HashMap, all three can be implemented with only slight order change.
def inorder(node): # left subtree -> node -> right subtree
if node.left: inorder(node.left)
print(node.val)
if node.right: inorder(node.right)
def postorder(node): # left subtree -> right subtree -> node
if node.left: postorder(node.left)
if node.right: postorder(node.right)
print(node.val)
def preorder(node): # node -> left subtree -> right subtree
print(node.val)
if node.left: preorder(node.left)
if node.right: preorder(node.right)
def preorder_iterative(root):
stack = [root]
while stack:
node = stack.pop()
if not node: continue
print(node.val)
stack.append(node.right)
stack.append(node.left)
def inorder_iterative(root):
node, stack = root, []
while stack or node:
while node:
stack.append(node)
node = node.left
node = stack.pop()
print(node.val)
node = node.right
def tree_dfs_iterative(root):
stack = [root]
visited = set()
while stack:
node = stack.pop()
if not node: continue
if node in visited: print(node.val); return
visited.add(node)
# stack.extend([node.right, node, node.left]) # inorder
# stack.extend([node, node.right, node.left]) # postorder
stack.extend([node.right, node.left, node]) # preorder
def tree_dfs_iterative(root):
stack = [(root, 0)]
while stack:
node, backtrack = stack.pop()
if node is None: continue
if backtrack: print(node.val); continue
stack.extend([(node.right, 0), (node, 1), (node.left, 0)]) # inorder
# stack.extend([(node.right, 0), (node.left, 0), (node, 1)]) # preorder
# stack.extend([(node, 1), (node.right, 0), (node.left, 0)]) # postorder
class BinaryTreeIterator:
def __init__(self, root, order='in'):
self.root = root
self.order = order
def _get_traverse_order(self, node):
if self.order == 'in': return [(node.right, 0), (node, 1), (node.left, 0)]
if self.order == 'pre': return [(node.right, 0), (node.left, 0), (node, 1)]
if self.order == 'post': return [(node, 1), (node.right, 0), (node.left, 0)]
def __iter__(self):
self.stack = [(self.root, 0)]
return self
def __next__(self):
if not self.stack: raise StopIteration
while self.stack:
node, backtrack = self.stack.pop()
if backtrack: return node.val
for item in self._get_traverse_order(node):
if item[0] is None: continue
self.stack.append(item)
for v in iter(BinaryTreeIterator(root, 'in')): print(v)
for v in iter(BinaryTreeIterator(root, 'pre')): print(v)
for v in iter(BinaryTreeIterator(root, 'post')): print(v)
BFS traversal
- BFS traversal with queue is quite straightforward.
def tree_bfs_iterative(root):
queue = deque([root])
while queue:
node = queue.popleft()
if not node: continue
print(node.val)
queue.extend([node.left, node.right])
def tree_bfs_iterative(root):
level = [root]
i = 0
while level:
next_level = []
for node in level:
print(node.val)
if node.left: next_level.append(node.left)
if node.right: next_level.append(node.right)
level = next_level
Augment the tree node
- Can be useful if we keep track of various information on node:
- pointer to parent node
- height / depth of the node
- size / min / max of the subtree / node to leaf path rooted at node
Some examples:
- Find root to target node path in pre order traversal.
def path_to_node(root, target):
path = []
stack = [(root, 0)]
while stack:
node, backtrack = stack.pop()
if not node: continue
if backtrack: path.pop()
else:
path.append(node)
if node.val == target: return node, path
stack.extend([(node, 1), (node.left, 0), (node.right, 0)])
return None, path
- Find Lowest common ancestor for two nodes
def lca(root, p_val, q_val):
p, path_to_p = path_to_node(root, p_val)
q, path_to_q = path_to_node(root, q_val)
for i in min(len(path_to_p), len(path_to_q)):
if path_to_p[i] != path_to_q[i]: break
else: lca = path_to_p[i]
return lca
- Annotate each node with parent pointer
def dfs_annotate_parent(root):
parent = {root: None}
stack = [root]
while stack:
node = stack.pop()
for child in node.left, node.right:
if child is None: continue
parent[child] = node
stack.append(child)
return parent
- Annotate each node with its height, where leaf nodes have height 0
def dfs_annotate_heights(root):
heights = {None: -1}
stack = [(root, 0)]
while stack:
node, backtrack = stack.pop()
if node is None: continue
if backtrack: heights[node] = max(heights[node.left], heights[node.right]) + 1
else: stack.extend([(node, 1), (node.left, 0), (node.right, 0)])
return heights
- Annotate each node with its depth
def bfs_annotate_depths(root):
depths = dict()
queue = deque([root])
depth = 0
while queue:
for _ in range(len(queue)):
node = queue.popleft()
depths[node] = depth
for child in node.left, node.right:
if child is None: continue
queue.append(child)
depth += 1
return depths
- Annotate each node with serialization of its subtree during postorder traversal
def create_node_to_subtree_struct_mapping(root):
stack = [(root, 0)]
subtrees = dict()
node_to_subtree = dict()
node_to_subtree[None] = "null"
while stack:
node, backtrack = stack.pop()
if not node: continue
if backtrack:
subtree = ",".join([str(node.val),node_to_subtree[node.left],node_to_subtree[node.right]])
subtrees.setdefault(subtree, []).append(node)
node_to_subtree[node] = subtree
else:
stack.extend([(node, 1), (node.left, 0), (node.right, 0)])
- Annotate each node with its node to leaf path statistics
def longest_consecutive(root):
max_length = 1
stack = [(root, 0)]
inc_length = defaultdict(int)
dec_length = defaultdict(int)
while stack:
node, backtrack = stack.pop()
if not node: continue
if backtrack == 0: stack.extend([(node, 1), (node.left, 0), (node.right, 0)])
else:
left_inc = left_dec = 1
if node.left:
if node.val == node.left.val - 1: left_inc += inc_length[node.left]
if node.val == node.left.val + 1: left_dec += dec_length[node.left]
right_inc = right_dec = 1
if node.right:
if node.val == node.right.val - 1: right_inc += inc_length[node.right]
if node.val == node.right.val + 1: right_dec += dec_length[node.right]
max_length = max(max_length, left_inc + right_dec - 1, left_dec + right_inc - 1)
inc_length[node] = max(left_inc, right_inc)
dec_length[node] = max(left_dec, right_dec)
return max_length