Linked List
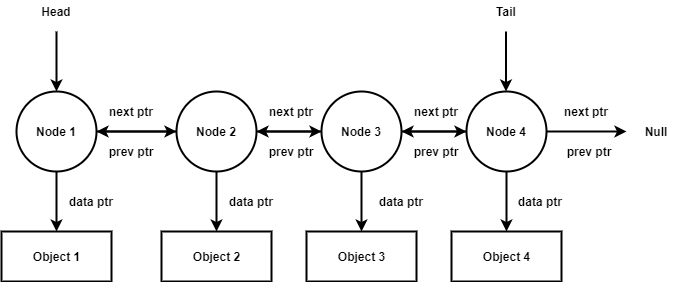
Remarks
- Linked List is a sequence of node objects where each node store pointers to
- some other node in the sequence
- the data this node is associated with
- Linked List can be used as the underline data structure for many common abstract data types like lists, stacks, queues, etc.
| operation | time |
|---|---|
| push at front | O(1) |
| pop at front | O(1) |
| push at back | O(1) |
| pop at back | O(N) |
| access via index | O(N) |
| insert in middle | O(N) |
| delete in middle | O(N) |
| swap two nodes | O(N) |
Common operations on singly linked list.
1 Node class for singly linked list.
class ListNode:
def __init__(self, item: Optional=None):
self.item = item
self.next = None
def __repr__(self) -> str:
return f"{super().__repr__()[:-1]} of {self.item} >"
nodes = list(map(ListNode, ['Head', 'Shoulders', 'Knees', 'Toes']))
for prev, next_ in zip(nodes, nodes[1:]):
prev.next = next_
head = nodes[0]
tail = nodes[-1]
del nodes
2 Traverse the linked list.
def traverse(head: ListNode, verbose: int=0) -> tuple[ListNode, int]:
curr = head
n = 0
while curr:
if verbose: print(curr.item)
if not curr.next: tail = curr
curr = curr.next
n += 1
return tail, n
# def traverse(head, k):
# def traverse(head, val):
assert traverse(head) == (tail, 4)
3 Push and pop node at front.
def push_front(head, node):
node.next = head
return node
def pop_front(head):
return head.next
node = ListNode('Hat')
head = push_front(head, node)
assert head == node and traverse(head)[1] == 5
head = pop_front(head)
assert head == node.next and traverse(head)[1] == 4
4 Push and pop node at back.
def push_back(tail, node):
tail.next = node
return node
def pop_back(head, tail):
curr = head
while curr.next is not tail: curr = curr.next
curr.next = None
tail = curr
return tail
node = ListNode('Shoes')
tail = push_back(tail, node)
assert tail == node and traverse(head)[1] == 5
tail = pop_back(head, tail)
assert traverse(head)[1] == 4 and tail.next == None
5 Insert and delete nodes in the middle.
def get(head, i):
curr = head
prev = None
while curr and i:
i -= 1
prev = curr
curr = curr.next
return prev, curr
def insert(head, i, node):
prev, next_ = get(head, i)
prev.next = node
node.next = next_
def erase(head, i):
prev, curr = get(head, i)
prev.next = curr.next
node = ListNode('Belly Button')
insert(head, 2, node)
assert get(head, 2)[1] == node and traverse(head)[1] == 5
erase(head, 2)
assert get(head, 2)[1] == node.next and traverse(head)[1] == 4
6 Swap nodes.
def swap(head, i, j):
i, j = sorted([i, j])
prev_i, node_i = get(head, i)
prev_j, node_j = get(node_i, j-i)
if prev_i:
prev_i.next = node_j
else:
head = node_j
prev_j.next = node_i
node_i.next, node_j.next = node_j.next, node_i.next
return head
old_head = head
head = swap(head, 1, 0)
head = swap(head, 2, 3)
head = swap(head, 3, 2)
head = swap(head, 0, 1)
assert head == old_head
7 Reverse Linked List.
def reverse(head):
prev = None
trav = head
while trav: trav.next, prev, trav = prev, trav, trav.next
return prev
Common Problems
- Two Pointers
- left, right - Palindrome
- slow, fast - cycle, last k
- Multiple Lists
- Merge, Intersection
- Search and Sorting
- Implement Stack/Queue/Deque etc.
- Doubly Linked List + Hash Table
Sample Questions
Implementation
Operations on Linked List
- 876. Middle of the Linked List
- 19. Remove Nth Node From End of List
- 25. Reverse Nodes in k-Group
- 206. Reverse Linked List
- 92. Reverse Linked List II
- 143. Reorder List
- 21. Merge Two Sorted Lists
- 23. Merge k Sorted Lists
Two Pointers
- 141. Linked List Cycle
- 160. Intersection of Two Linked Lists
- 234. Palindrome Linked List
- 2. Add Two Numbers